������Ӌ���I���S�����g�IJ���ͻ�ƣ����әC���W����Quantum Machine Learning�� QML����������ʵ��Ӧ�á�����������ͳ����ѧϰ���������ż���ƿ�������ݴ����ľ����ԣ�������Ӌ�������Ϊ��һ��������˾��DZ�����ر��ǣ�������}�Ľ�Q�����У������㷨���@ʾ���@���ă��ݡ�
��������Ӌ����IJ��Ͻ��������әC���W����QML���Ѿ���Ϊ�������ѧ�����һ�������о������ر����ڴ������ģ���ݼ���ѵ������ģ�ͺ��Ż����ྫ�ȵȷ��棬����Ӌ��չ��������ͳ������������DZ����Ȼ������ν�������ѧ�Ķ������ԣ������ӵ����������ʵ��Ӧ���ڼලѧϰ�ͷ�������һֱ�Ǹ������һ����ս��
��������ƌW�҂�����˸��N�����㷨����Q����C���W���е�����Ȼ����������F�м��g��Ȼ���ڌ�����Ӳ���ĸ�Ҫ���Ӌ���}�s���^�ߵĆ��}�����˿˷��@Щ���ƣ��㷨�Ƽ���NASDAQ:MLGO���㷨���g��˾�����һ�N�������Ӽm�p������Ӗ���㷨�����O�����ӷ�����ļm�p�o��Ӗ���㷨��߀����˻���ؐ������ʽ�ijɱ�������ʹ�ö���Ӗ���ӱ����`���܉�ͬ�r�õ����a���Ķ���Խ�˂��y�㷨������߅�磬���O�����ӷ�����ṩ��һ����Ч�Ҿ��ЏV������ǰ���Ľ�Q������
�㷨�Ƽ��O�����ӷ�����ļm�p�o��Ӗ���㷨�ĺ������ڣ��������Ӽm�p�F����һ���܉�ͬ�r��������Ӗ���ӱ�����˺���ģ�͡��c���y�ęC���W��������ͬ�����ӷ�������H��̎���һ�ӱ�����Ϣ��߀�������Ӡ�B�Ќ������ӱ��M�ЁK��̎�����Ķ��O������Ӗ��Ч�ʡ�
ԓ�㷨ͨ�^���ӯB�ӑB������Ӗ���ӱ���ʾ�����ӱ��أ�qubit���������Kͨ�^�����T�������@Щ�ӱ��Ę˺���Ϣ���a�����ӑB�С��������ӱ���֮�g�ļm�p�Pϵ��������܉���ͬһ�r�g��ͬ�r�������ӱ��M�в������@һ����ʹ�Â��y�������ӱ�̎�����������ƣ��O�������Ӗ���ٶȺͷ��Ч����
���⣬�㷨������һ������ؐ������ʽ�ijɱ�������ؐ������ʽ���������W��һ���Ҫ�Ķ��������C�������Ӽm�p�c������Ϣ̎����ʽ֮�g�ą^�e��ͨ�^�������ӱ��ķ���e�`ͬ�r���a�ڳɱ������У������^�̲��H�H�����چ�һ�ӱ����e�`��������ͬ�r���]�����ӱ������w���F���@�N�����˷��˂��y�㷨�еľֲ��������}��ʹ�÷���ȴ��������
�㷨�Ƽ��ල���ӷ������ľ�������ѵ���㷨��ʵ�������ڵ�ǰ����Ӌ�㼼���ļ��������ɲ���:���ӱ��ء������Ų����Լ����Ӳ�����ͨ����Щ�����������㷨�ܹ�������Ӌ����϶��������ݽ��и�Ч������
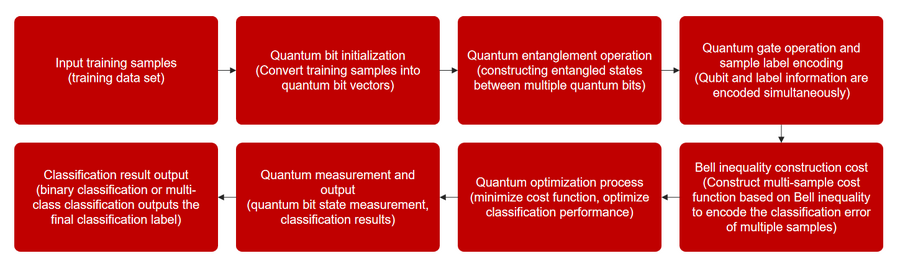
���ӱ��صı�ʾ�c��ʼ��:���㷨�ij�ʼ�A�Σ�ݔ���Ӗ���ӱ������D�������ӱ��ء�ÿ��Ӗ���ӱ�����һ����������ӱ��أ��@Щ���ؕ�����ʼ�����ض������ӑB�����ˌ��F�m�p���������ӱ���֮�g���M�мm�p�������Ա��������m���E�й�ͬ̎��ӱ�������
���Ӿ����Ĺ���:���Ӿ���������Ӌ��ĺ�������֮һ���ڱ��㷨�У�ѵ�������ᱻ���ų�һ������̬������ζ������֮�����Ϣ��ͨ�����Ӿ����������ʹ�������һ���̲�����������ݴ�����Ч�ʣ����ܹ�����ѵ�������е�������
ؐ������ʽ�đ����c�ɱ������ă���:���Ӽm�p��һ���P�I������ؐ������ʽ�����㷨�У�ؐ������ʽ�����ژ����ɱ�������Ŀ������С������e�`���c���y������ͬ���@һ�ɱ������܉�ͬ�r���]���Զ����ӱ����e�`��ʹ�Ã����^���܉�ͬ�r�Pע���Иӱ��ı��F�������ǃH�H�����ӱ��M�Ѓ�����ͨ�^�����㷨�Ŀ�����⣬�ɱ��������Ը�Ч�ر���С�����Ķ��õ������Y����
�������Ľ�������:���գ�ͨ�����Ӳ������㷨�������Y�����ڶ�Ԫ���������У�����ζ�������ѵ�������ᱻ��Ϊ���࣬���ڶ�����������У�������������Ϊ����������Ӌ������������䲢�д���������������ϵͳ�ڽ϶̵�ʱ������ɸ��ӷ�������
ԓ���g����������������ܹ��������Ӿ����Ķ������ʣ�ʹ��ѵ�������ڶ��ѵ��������ʵ�ֲ��л����ⲻ�������ѵ���ٶȣ����ܹ���Ч��߷��ྫ�ȣ��ر������������Ӵ�������У���ͳ�������ܻ����ټ���ƿ����������Ӌ�����ܹ�����ͻ����Щ���ơ�
���⣬����ؐ������ʽ�ijɱ���������Փ�ϱȂ��y���`����С���������ӽ��ѣ�����ͬ�r̎������Ӗ���ӱ����`������˂��y�����п��ܳ��F�ľֲ�����}���@ʹ�ñO�����ӷ�������}�s����΄��б��F��ɫ��
Ȼ��������Ӌ�㼼����Ȼ����������ս�����磬����Ӌ������ȶ��Ժͼ����ģ��Ȼ���������أ����ӱ��ص�����������ʶ�����Ӱ���㷨��ʵ��Ч������ˣ��������������Ӌ��ƽ̨��ʵ�ָ�Ч���㷨��Ȼ��һ����Ҫ��һ�����˵ļ������⡣
��������Ӌ�㼼���IJ��Ϸ�չ�����әC���W���ؽ���Ϊδ���Ƽ����µ���Ҫ�����㷨�Ƽ���NASDAQ:MLGO���ල���ӷ������ľ�������ѵ���㷨Ϊ��һ�������µĿ����ԡ�ͨ�������Ӿ����봫ͳ�ķ����㷨��ϣ��ü��������ѵ��Ч�ʡ���ǿ���ྫ�ȷ���չʾ���˾�DZ������������Ӌ��������������ս��������Ӳ���Ľ����������о��IJ�������������������ţ�����Ӌ�㽫�ڻ���ѧϰ��������һ��������δ�������ӷ��������ܲ������ڴ�ͳ�Ķ�Ԫ�������������п����ڸ�Ϊ���ӵ�����չ�ֳ��ɱ�������ơ�
���ƏV��

